解説
解説は書けたら書きます
問題
K種類の絵具を良い感じに混ぜて、H種類の目標色を順番に渡す問題
NxNマスを自由に仕切ったり繋げて良いが、Tターンまでしか行動できない
参加記
最初の考察
最近は自分用のdiscordを作って、適当に書き連ねてメモとしています
そのまま貼りますので興味のある方はどうぞ


AI実装
週末疲れ+子供の寝かしつけのため、布団の中でスマホコーディングすることにしました
実際には、ChatGPTに考察を投げて実装してもらうだけですが...
1gずつ使う貪欲
どれくらい使い物になりそうか確かめるため、1g出して1g提供する貪欲をpythonで書いてもらいました
得点109,690,905を得て、相対順位は大体3Gでした
今の得点からおよそ1/14にすれば1位相当だなと思っていました
複数絵具を混ぜる貪欲
2x2サイズの容量4のウェルに固定して、3色まで追加して目標色に近づける貪欲を書いてもらいました
得点18,092,839を得て、1ページ目に入っていました
4色まで絵具を混ぜる貪欲
2x2のサイズはそのままに、4色まで追加するコードを書いてもらいました
また、D*0.1*n/H (nは現在の使用絵具量)を絵具の使用コストにしました
手元では明らかに改善しましたが、提出するとTLEでした(AC 11ケース)
K=20から4つを選ぶ重複組み合わせは、8,855組ありこれだけなら計算は間に合いますが、H=1,000 x ウェル数100 が乗ると流石に間に合わないようでした
計算量改善をお願いすると、KD-Treeで最近傍探索をすると間に合うと言われたので、目標色の近くL個を選んで評価してもらいます
得点13,009,463を得て、相対スコア23Gで8位になりました
隣接を一瞬接続して戻す
あまり効くイメージが無いですがお試しで
使用コストをD*0.05*n/Hに変更もしてみました(絵具をより使っても色を合わせに行く
得点11,906,526と伸びましたので効果はあったようです
隣接を接続して、戻したうえで絵具を足す
上記が効いたのならと、評価する行動を増やします
得点10,666,560とちょっと伸びました
また、左に区切りを入れておいて、下or右に区切りを入れると現在の量の50%、75%を使用して色を作る遷移も入れてみました
現状のseed=0の最終状態は下のような感じです

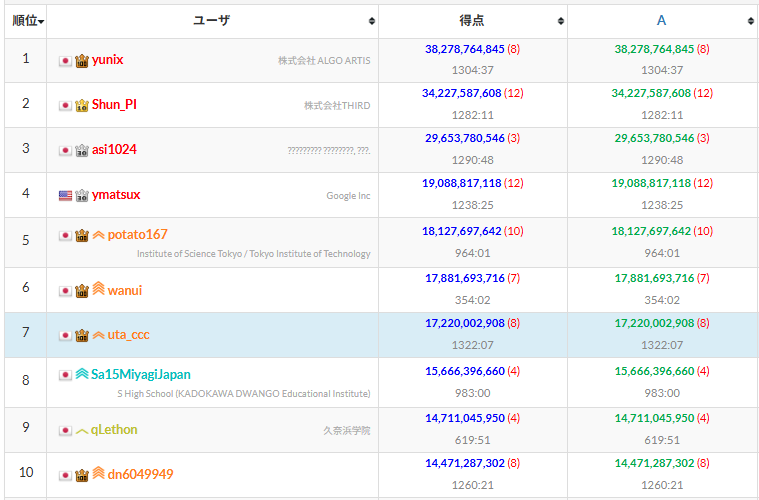
土曜日の夕方あたりの順位表です
7位にも関わらず、17Gしかないのでまだまだ伸びしろがある問題なようです
調査フェーズ
seed=0では、score=188,194が出ていて、うち誤差が142,329 絵具が45,864です
合計の誤差量は14.232936となっていますが、ケースごとの値を見てみます
seed=は0 (K=4, D=3822)絵具コストが高いため、後半程色合わせに苦労している様子が見えます
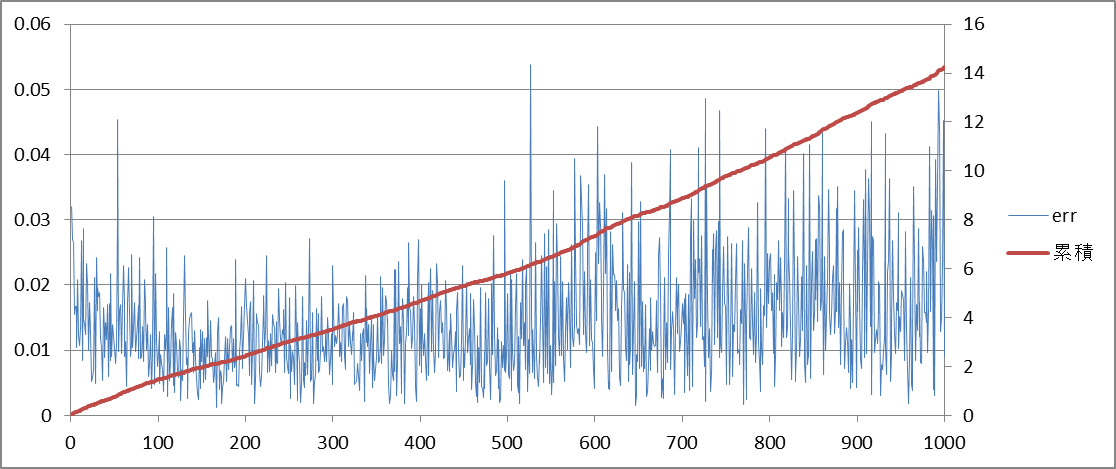
seed=11です(K=20, D=47)
最初の数ケースで大きめの誤差が出ており、あとは同じような感じに見えます
絵具コストが低いと最後まで色合わせを頑張っているみたいです

絵具コストは全体の1/5程度のため、1位相当になるには誤差を1/4~1/5まで減らさないといけないようです(驚愕
エクセルで実験
seed=0の2ケースについてソルバーで理想の混ぜ比率を出してみると以下のようになりました

さらに手動で操作を最適化すると、
- 容量20のウェルにK=2の絵具を1g出す
- 容量2と18に分割して、容量18側を捨てて分割を戻す(1/10の濃度)
- K=1の絵具を1g出し、容量1と19に分割する
- K=0の絵具を容量19側に1g出し、容量1と18に分割する
- K=3の絵具を容量18に1g出す
すると、誤差0.000891の色を作ることが出来ます
上手く分割をして濃度を調整して、色を混ぜていくことが大事そうです
ただ、操作回数が増えるため注意が必要そうです
意気揚々と実装を開始しますが躓きました
下のように、容量20や容量400のウェルにして、任意濃度を作って...を試しましたが、実装に手こずるのと、思ったよりスコアが出ないため一旦諦めました
ただ、分割で濃度を操作するのは流石に必須な気もするので、別の形を考えます

貪欲解の行動評価
貪欲解が実際に行動として選択した内容をカウントしました

回数の多かった順に、どんな操作か書くと
- merge_add2:ウェル2つをマージして絵具追加、目標色提供後マージ解除
- merge_add:ウェル2つをマージし、マージ解除後に絵具追加、目標色提供
- merge_take:ウェル2つをマージし、そのまま目標色提供
- add:そのまま絵具追加、目標色提供
- take:そのまま目標色提供
ほぼマージ操作が絡んでおり、結構想定外でした
チューブ色の凸包内に目標色がほぼ入っていることを考えると、平均を取る行動だけでも目標に近づきやすい上、微調整の役割も担えているようです
マージ戦略の強化
現状は隣接ウェル2つのマージしか行っていないため、これを増やしてみます
3つ4つと増やすにつれて、スコアも上がりますが時間も伸びます
下のように4つのウェルがちゃんと繋がっている様子もビジュアライザで確認できました
ただ、操作数も増えるため、入力の値に応じて切り替えないと厳しそうです

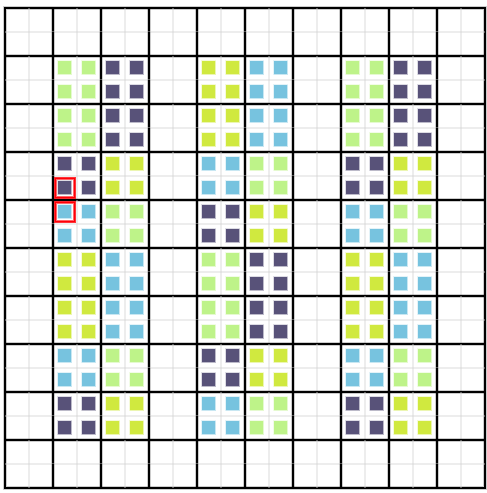
初期盤面に色を散りばめる
ビジュアライザを見ていると、新しい領域を使って色を作っている場面があまりなく、既存の色をマージしていることがかなり多いことに改めて気付きました
そこから、最初から絵具を適当に置いておけばいい感じに使ってくれるのでは。と考えて1gずつ置いてみるとスコアが上がりました
絵具の混合を考える
CMYを、3次元ベクトルとして捉えると見通しが良さそうですが、ChatGPTに聞くと凸結合などと言われますが正直良く分かりません
一旦2次元ベクトルで考えてみると割と納得できた気がしたので書き残します
2色混ぜる場合、その比率で平均する(加重平均)ので、ベクトル同士を結んだ点線上の色を作ることが出来ます(これを凸結合と呼ぶらしい)
3色混ぜる場合、ベクトル同士を結んだ点線三角形の中の色を作ることができます

これを3次元に戻して考えてみると、次元が1つ増えるため4色を任意の比率で混ぜることで目標色が作れそうです
この4色による凸包が目標色を含んでいることが前提です
ただ、毎回4色を使う、かつ任意の比率で混ぜれるわけでないことに気付いてしまいました...
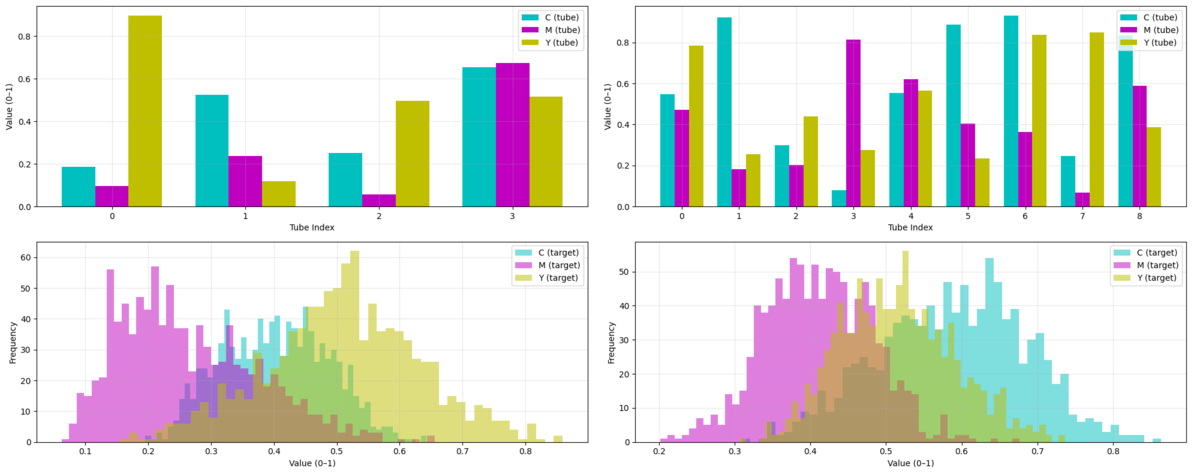
チューブ本数による違い
seed=0, 1 を並べました
入力生成方法から読み取るべきでしたが、チューブの傾向に結構引っ張られていて目標色が作りやすいようになっているようです
色ごとに合わせやすさの係数を掛けると、若干スコアが上がりそうでした
方針再検討

ChatGPTがカッコいい事を言っています。やりたいことはその通りです
2x2のウェルで固定すると、多様性は増しますが終盤に無駄な余りが結構出てしまいます
最後、余りを減らすため4x4の区切りに広げることでもったいない絵具を減らしてみました
Dが小さいケースでは、最後まで色を合わせに行く方が良さそうだったため、Dの値で実施するかは切り替えました
他に量を調整しつつ上手い事やれる方針がないかな、と考えてみましたが
........色々検討して気付いたら最後の週末でした
chokudaiサーチ
現状、評価値貪欲だけで500msec使っており全体でビームサーチなどを走らせる余裕はありません
最終盤だけなら?と思い、実装が簡単なchokudaiサーチを取り入れました
実装自体はAHC038で経験済みなので、2時間程度で動くものは出来ましたがスコアが伸びません
なんなら評価値貪欲だけの方が強い状態です
探索するノードを選ぶにあたって盤面評価をする必要があるのですが、これがまた難しい
最終スコアで評価すると絵具を使わないことが重視され過ぎて、累積エラー率で評価すると絵具が使われ過ぎるという困った状況です
最終的に、絵具の使用コストは sqrt(D)に、使用量の傾斜を変化させたものを使いました
こういったものはOptunaで最適化するべきですが、めんどくさがって今回もやれませんでした
最終ビジュアライザ
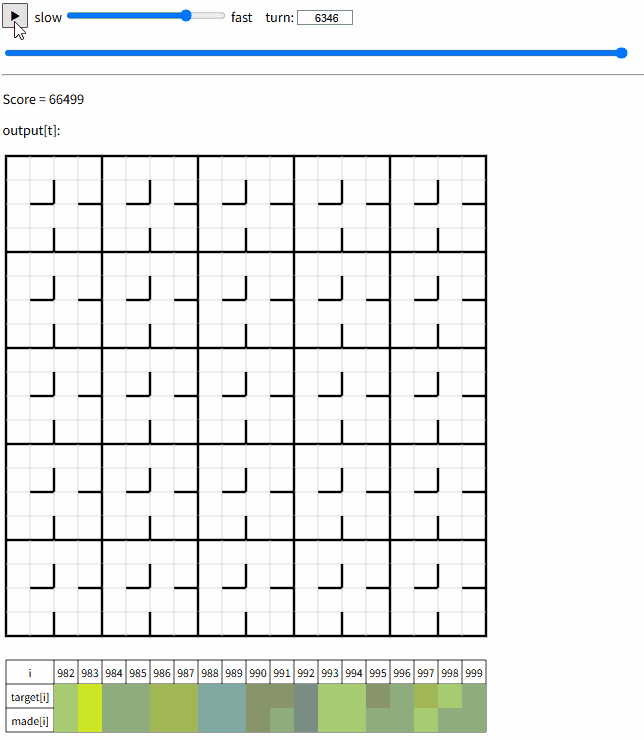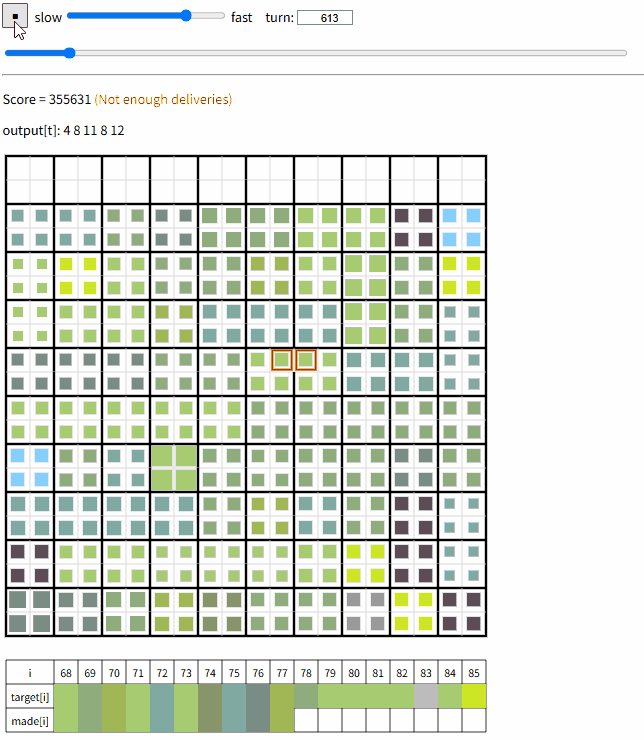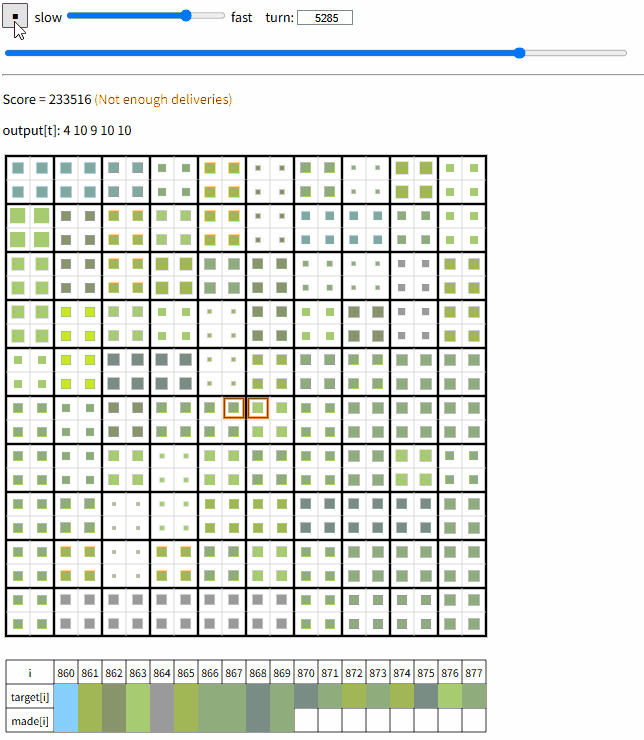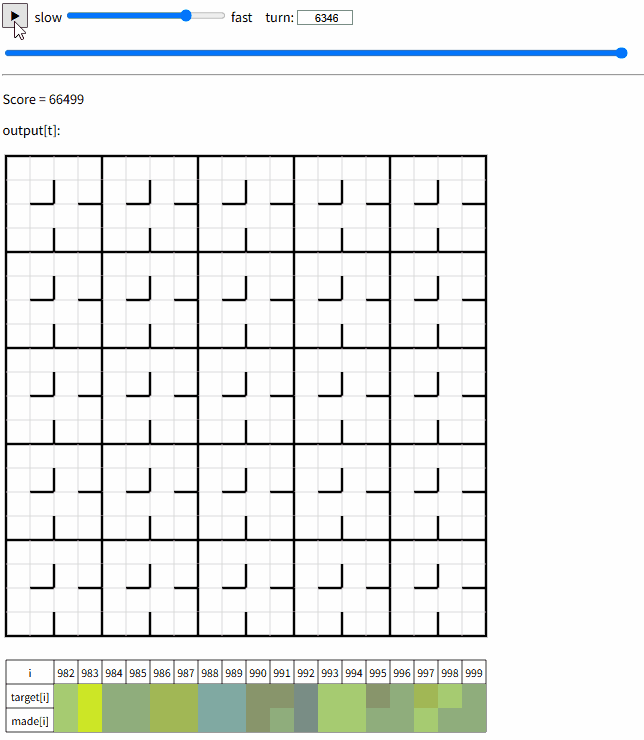
シード毎のスコア
今回、TやDといったパラメータによってスコアが大きくばらつくようでした
期間中はあまり気にしていなかったのですが、極端に差のつくケースがあるかどうかは順位に影響するので探してみても良かったように思います
seed0 = 66,499
seed1 = 91,256
seed2 = 206,553
seed3 = 78,617
seed4 = 121,631
seed5 = 101,294
seed6 = 79,377
seed7 = 131,733
seed8 = 201,698
seed9 = 82,908
おわりに
問題のパラメータによって最適な解法が色々ありそうな、面白い問題で今回も楽しめました!
結局実装できたのは正方形区切りだけでしたが、過程では最上位の方針と近いことを考えることも出来ていました
なんとなくできそうだな。から実装まで持っていく実力がまだまだ足りていないと感じました
今回は時間減衰に勝てそうですが、ジリ貧になりつつあるので力を付けてもうひと伸びしたいですね!